Clear the basic studies already done in 1st n 2nd year of bsc subject then go through the syllabus and note down the things u know then u cann make ur own notes  and google will help u in that as per a tutor take help of best IT tutor for hard topics  who can make you understand better than 1st

#include
using namespace std;

int sum(int a,int b)
{
   return a+b;
}
void f2(int (*f)(int,int),int a,int b) //'*f' is a POINTER TO A FUNCTION whose RETURN TYPE is                                                           //'int' and arg type (int,int)  . Here, '*f' is FORMAL PARAMETER
{                                                                
  cout<<sum(a,b)<<endl;
}
int main()
{   int (*p1)(int,int)=∑          //Here, '*pf1' is ACTUAL PARAMETER
    f2(sum,10,20);                         //NAME OF A FUNCTION IS ITSELF A POINTER TO ITSELF
    f2(p1,20,79);
    return 0;

}

Java 9 is here! A major feature release in the Java Platform Standard Edition is Java 9

Lets see what more it offers more than its previous versions

• Java platform module
• JEP 223 : New version string scheme

Moreover it includes enhancements for microsoft windows and MAcOS OS platforms

1. Choose the pivot (using the "median-of-three" technique); also, put the smallest of the 3 values in A[low], put the largest of the 3 values in A[high], and swap the pivot with the value in A[high-1]. (Putting the smallest value in A[low] prevents right from falling off the end of the array in the following steps.)
2. Initialize: left = low+1; right = high-2
3. Use a loop with the condition:

while (left <= right)

The loop invariant is:

all items in A[low] to A[left-1] are <= the pivot
all items in A[right+1] to A[high] are >= the pivot

Each time around the loop:

left is incremented until it "points" to a value > the pivot
right is decremented until it "points" to a value < the pivot
if left and right have not crossed each other,
then swap the items they "point" to.

1. Put the pivot into its final place.

Deadlocks in Distributed Systems:

Deadlock can occur whenever two or more processes are competing for limited resources and the processes are allowed to acquire and hold a resource (obtain a lock) thus preventing others from using the resource while the process waits for other resources.

Two common places where deadlocks may occur are with processes in an operating system (distributed or centralized) and with transactions in a database.

• Deadlocks in distributed systems are similar to deadlocks in single processor systems, only worse:

  • They are harder to avoid, prevent or even detect.

  • They are hard to cure when tracked down because all relevant information is scattered over many machines.

• People sometimes might classify deadlock into the following types:

  • Communication deadlocks : Competing with buffers for send/receive

  • Resources deadlocks : Exclusive access on I/O devices, files, locks, and other resources

• Four best-known strategies to handle deadlocks:

  • The ostrich algorithm (ignore the problem).

  • Detection (let deadlocks occur, detect them, and try to recover).

  • Prevention (statically make deadlocks structurally impossible).

  • Avoidance (avoid deadlocks by allocating resources carefully).

Deadlock Detection:

Deadlock detection attempts to find and resolve actual deadlocks.  These strategies rely on a Wait-For-Graph (WFG) that in some schemes is explicitly built and analyzed for cycles.   In the WFG, the nodes represent processes and the edges represent the blockages or dependencies.  Thus, if process A is waiting for a resource held by process B, there is an edge in the WFG from the node for process A to the node for process B. 

 In the AND model (resource model), a cycle in the graph indicates a deadlock.  In the OR model, a cycle may not mean a deadlock since any of a set of requested resources may unblock the process.  A knot in the WFG is needed to declare a deadlock.  A knot exists when all nodes that can be reached from some node in a directed graph can also reach that node.

In a centralized system, a WFG can be constructed fairly easily.  The WFG can be checked for cycles periodically or every time a process is blocked, thus potentially adding a new edge to the WFG.   When a cycle is found, a victim is selected and aborted.

 Centralized Deadlock Detection:

 We use a centralized deadlock detection algorithm and try to imitate the nondistributed algorithm.

• Each machine maintains the resource graph for its own processes and resources.

• A centralized coordinator maintain the resource graph for the entire system.

• When the coordinator detect a cycle, it kills off one process to break the deadlock.

• In updating the coordinator’s graph, messages have to be passed.

• Method 1) Whenever an arc is added or deleted from the resource graph, a message have to be sent to the coordinator.

• Method 2) Periodically, every process can send a list of arcs added and deleted since previous update.

• Method 3) Coordinator ask for information when it needs it.

False Deadlocks :

• When the coordinator gets a message that leads to a suspect deadlock:

• It send everybody a message saying “I just received a message with a timestamp T which leads to deadlock. If anyone has a message for me with an earlier timestamp, please send it immediately”

• One possible way to prevent false deadlock is to use the Lamport’s algorithm to provide global timing for the distributed systems.

• When every machine has replied, positively or negatively, the coordinator will see that the deadlock has really occurred or not.

The Chandy-Misra-Haas algorithm:

• Processes are allowed to request multiple resources at once the growing phase of a transaction can be speeded up.

• The consequence of this change is a process may now wait on two or more resources at the same time.

• When a process has to wait for some resources, a probe message is generated and sent to the process holding the resources. The message consists of three numbers: the process being blocked, the process sending the message, and the process receiving the message.

• When message arrived, the recipient checks to see it it itself is waiting for any processes. If so, the message is updated, keeping the first number unchanged, and replaced the second and third field by the corresponding process number.

• The message is then send to the process holding the needed resources.

• If a message goes all the way around and comes back to the original sender -- the process that initiate the probe, a cycle exists and the system is deadlocked.

• There are several ways to break the deadlock:

• The process that initiates commit suicide : this is overkilling because several process might initiates a probe and they will all commit suicide in fact only one of them is needed to be killed.

• Each process append its id onto the probe, when the probe come back, the originator can kill the process which has the highest number by sending him a message. (Hence, even for several probes, they will all choose the same guy)

The Probe Scheme:

The scheme proposed by Chandy, Misra and Haas [1] uses local WFGs to detect local deadlocks and probes to determine the existence of global deadlocks.  If the controller at a site suspects that process A, for which it is responsible, is involved in a deadlock it will send a probe message to each process that A is dependent on.  When A requested the remote resource, a process or agent was created at the remote site to act on behalf of process A to obtain the resource.  This agent receives the probe message and determines the dependencies at the current site.

The probe message identifies process A and the path it has been sent along.  Thus, the message probe(i,j,k) says that it was initiated on behalf of process i and was sent from the controller for agent j (which i is dependent on) to the controller for agent k.

When an agent whose process is not blocked receives a probe, it discards the probe.  It is not blocked so there is no deadlock.   An agent that is blocked sends a probe to each agent that it is blocked by.  If process i ever receives probe(i,j,i), it knows it is deadlocked.

This popular approach, often called "edge-chasing", has been shown correct in that it detects all deadlocks and does not find deadlocks when none exist.

In the OR model, where only one out of several requested resources must be acquired, all of the blocking processes are sent a query message and all of the messages must return to the originator in order for a deadlock to be declared.  The query message is similar to a probe, but has an additional identifier so the originator can determine whether or not all the paths were covered.

There are several variations to these algorithms that seek to optimize different properties such as: number of messages, length of messages, and frequency of detection. One method proposed by Mitchell and Merritt for the single-resource model, sends information in the opposite direction from the WFG edges .

Deadlock Prevention:

Prevention is the name given to schemes that guarantee that deadlocks can never happen because of the way the system is structured.   One of the four conditions for deadlock is prevented, thus preventing deadlocks. 

Collective Requests:

One way to do this is to make processes declare all of the resources they might eventually need, when the process is first started.  Only if all the resources are available is the process allowed to continue.  All of the resources are acquired together, and the process proceeds, releasing all the resources when it is finished.  Thus, hold and wait cannot occur.

The major disadvantage of this scheme is that resources must be acquired because they might be used, not because they will be used.  Also, the pre-allocation requirement reduces potential concurrency.

Ordered Requests

Another prevention scheme is to impose an order on the resources and require processes to request resources in increasing order.  This prevents cyclic wait and thus makes deadlocks impossible.

One advantage of prevention is that process aborts are never required due to deadlocks.  While most systems can deal with rollbacks, some systems may not be designed to handle them and thus must use deadlock prevention.

• A method that might work is to order the resources and require processes to acquire them in strictly increasing order. This approach means that a process can never hold a high resource and ask for a low one, thus making cycles impossible.

• With global timing and transactions in distributed systems, two other methods are possible -- both based on the idea of assigning each transaction a global timestamp at the moment it starts.

• When one process is about to block waiting for a resource that another process is using, a check is made to see which has a larger timestamp.

• We can then allow the wait only if the waiting process has a lower timestamp.

• The timestamp is always increasing if we follow any chain of waiting processes, so cycles are impossible --- we can used decreasing order if we like.

• It is wiser to give priority to old processes because

  • they have run longer so the system have larger investment on these processes.

  • they are likely to hold more resources.

  • A young process that is killed off will eventually age until it is the oldest one in the system, and that eliminates starvation.

Preemption:

Wait-die Vs. Wound-wait:

• Definition it can be restarted safely later.

i. Wait-die:

• If an old process wants a resource held by a young process, the old one will wait.

• If a young process wants a resource held by an old process, the young process will be killed.

• Observation: The young process, after being killed, will then start up again, and be killed again. This cycle may go on many times before the old one release the resource.

• Once we are assuming the existence of transactions, we can do something that had previously been forbidden: take resources away from running processes.

• When a conflict arises, instead of killing the process making the request, we can kill the resource owner. Without transactions, killing a process might have severe consequences. With transactions, these effects will vanish magically when the transaction dies.

ii. Wound-wait:

• If an old process wants a resource held by a young process, the old one will preempt the young process, wounded and killed, restarts and wait.

• If a young process wants a resource held by an old process, the young process will wait.

What is Complexity Analysis of Algorithm?

Complexity Analysis, simply put, is a technique through which you can judge about how good one particular algorithm is.  Now the term “good” can mean many things at different times.

Suppose you have to go from your home to the Esplanade! There are many ways from your home that may lead to Esplanade. Take any one, and ask whether this route is good or bad. It may so happen that this route is good if the time of travel is concerned (that is the route is short enough), but at the same time, it may be considered bad taking the comfort into considerations (This route may have many speed breakers leading to discomforts). So, the goodness (or badness as well) of any solution depends on the situations and whatever is good to you right now, may seem as bad if the situation changes. In a nutshell, the goodness/badness or the efficiency of a particular solution depends on some criteria of measurements.

So what are the criteria while analyzing complexities of algorithms?

Focusing only on algorithms, the criteria are Time and Space. The criteria Time, judges how fast or slow the algorithms run when executed; and the criteria Space judges how big or small amount of memory (on primary/hard disks) is required to execute the algorithm. Depending on these two measuring criteria, two type of Algorithm Analysis are done; one is called Time Complexity Analysis and the second one is Space Complexity Analysis.

Which one is more important over the other?

I am sorry! I do not know the answer; rather there is no straight forward answer to this question. Think of yourself. Thinking of the previous example of many solutions that you have for travelling from your home to Esplanade, which criteria is most important? Is it Time of Travel, or is it Comfort? Or is it Financial Cost? It depends actually. While you are in hurry for shopping at New Market, the Time Taken would probably be your choice. If you have enough time in your hand, if you are in jolly mood and if you are going for a delicious dinner with your friends, probably you would choose Comfort; and at the end of the month, when you are running short with your pocket money, the Financial Cost would be most important to you.  So the most important criterion is a dynamic notion that evolves with time.

Twenty or thirty years back, when the pace of advancement of Electronics and Computer Hardware was timid, computer programs were forced to run with lesser amount of memory.  Today you may have gigantic memory even as RAM, but that time, thinking of a very large hard disk was a day dreaming! So at that time, Space Complexity was much more important than the Time Complexity, because we had lesser memory but ample times.

Now the time has changed! Now a day, we generally enjoy large memories but sorry, we don’t have enough time with us. We need every program to run as quick as possible! So currently, Time Complexity wins over Space Complexity.  Honestly, both of these options are equally important from theoretical perspective but the changing time has an effect to these.         

What is Dynamic Programming?

Dynamic Programming, DP in short, is an intelligent way of solving a special type of complex problems which otherwise would hardly be solved in realistic time frame.

What is that special type of problems? 

DP is not best fit for all types of complex problems, it is well suited for the problems with following characteristics only:

1. The given problem must be decomposable in multiple smaller sub problems with similar nature.
2. Sub problems must also be decomposable into still sub problems and this nesting should continue till a stage arises when the current sub problems could be solved with least cost.
3. At any particular stage, the sub problems must be interdependent.
4. At any specific stage the problem could be solved by solving its sub problems.

So this is like Divide and Conquer. Isn't it?

Wait. Don't jump into any conclusion right now. We have not studied the DP procedures yet! we are currently studying the nature of DP problems only. So it will be too early to compare Divide and Conquer with DP.

But this is true, that just a mere look at the characteristics of DP problems gives a feeling that DP is close to Divide and Conquer. But there is a MAJOR difference, in Divide and Conquer, at any stage, the sub problems enjoy No Inter-Dependencies.

Let us put this on hold. We will revert back to this topic once more only after we have got some experience in DP. But for the time being, take it from me that DP and Divide & Conquer are not same.

Why do not you say how DP works? 

DP works as simple as possible. After the problem is broken down to trivial sub-problems in levels, DP starts solving the sub problems bottom up. Once a sub problem is solved, solution is written down (saved) into a table so that if the same sub problem reappears, we get a ready made solution. This is done in every level.

What is so special about this process?

Yes. It is special. See while you decompose a problems into sub problems, sub problems into sub sub problems and so on, you ultimately reach to a point when you need to solve the same sub problems many a times. And this "many" is not a child's play in real life. Lots of computational resources are unnecessarily spent on this which makes the process sluggish with poor time complexity values. 

With DP you can avoid the re computations of the same sub problems.This will save a lot of time and other computational resources. But there are table look ups for solving reappearing sub problems, and this is not going to offer a bed of roses. This will surely take some time, but with hashing and some other smart alternatives,  table look ups can be made easy. 

Getting out of my head! Show me how DP works with an example. 

 Lets think of Fibonacci series. We know that Fib(n) = Fib(n-1) + Fib(n-2). Hence to compute Fib(4),

Fib(4) = Fib(3) + Fib(2)

          = (Fib(2) + Fib(1)) + Fib(2)

          = ((Fib(1) + Fib(0)) + Fib(1)) + Fib(2)

          = ((Fib(1) + Fib(0)) + Fib(1)) + (Fib(1) + Fib(0))

This could easily be done with Divide and Conquer with recursion. But there will be several call for the trivial case Fib(1) and Fib(0).

But in DP style we can think that

                                                          Fib(4)  ------------------- level 0

                                                   Fib(3) + Fib(2) ------------------ level 1

                                          Fib(2) + Fib(1)-------------------------- level 2

                                 Fib(1) + Fib(0) -------------------------------- level 3

 There will be only two calls of Fib(1) and Fib(0) altogether (shown in violet at level 3). The second Fib(1) (shown in red at level 2) will not be called at all as the result of that is already with us. Similarly Fib(2) (shown in green at level 1) will not be called at all as it has already been computed at level 2. In this way we could avoid re-computations in two occasions.

This is the strength of DP. This strength seems trivial with this trivial example, but as the problem size will grow, this strength will seem to have prominent advantage.  Just Think of fib(100)

Is Dynamic Programming a process to find solution quicker?

Yes it is, but the nature of the solution we are talking to is an optimal solution not the exact one. The principle of optimality applies if the optimal solution to a problem always contains optimal solutions to all subproblems . Take the following example:

Let us consider the problem of making N Rupees with the fewest number of Rupee coins.

Either there is a coin of value N Rupees (Exact Solution), or the set of coins making up an optimal solution for N Rupees can be divided into two nonempty subsets, n₁ Rupees and n₂ Rupees (Optimal Solution).

If any of the n₁ Rupees or n₂ Rupees, can be made with fewer number of coins, then clearly N can be made with fewer coins, hence solution was not optimal.

Tell me more on Principle of Optimality:

The principle of optimality holds if

Every optimal solution to a problem contains optimal solutions to all subproblems

The principle of optimality does not say

If you have optimal solutions to all subproblems then you can combine them to get an optimal solution

Example: If we have infinite numbers of coins of 1cents, 5 cents, 10 cents only then optimal solution to make 7 cents is 5 cents + 1 cent + 1 cent, and the optimal solution to make 6 cents  is 5 cents + 1 cent, but the optimal solution to make 13 cent is NOT 5 cents + 1 cent + 1 cent + 5 cents + 1 cent

But there is a way of dividing up 13 cents into subsets with optimal solutions (say, 11 cents + 2 cents) that will give an optimal solution for 13 cents. Hence, the principle of optimality holds for this problem.

Let us see one example where Principle of Optimality does not hold.

In the following graph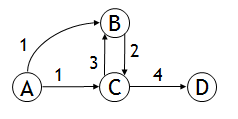

The longest simple path (path not containing a cycle) from A to D is A->B->C->D. However, the sub path A->B is not the longest simple path from A to B (A->C->B is longer)

The principle of optimality is not satisfied for this problem. Hence, the longest simple path problem cannot be solved by a dynamic programming approach.

Can you give me a thorough example of DP? 

Why not! Following is an example of working of Dynamic Programming. It presents a comparative analysis of working of DP with the working of Divide & Conquer.

Let us consider the Coin Counting Problem. It is to find the minimum number of coins to make any amount, given a set of coins.  

If we are given with a set of coin of 1 unit, 10 units and 25 units, then to make 31, how many minimum numbers of coins are required?

Let us check whether the greedy method will work or not. Greedy Method says that just choose the largest coin that does not overshoot the desired amount. So at the first step, we will take one coin of 25 units and then successively in each of next six steps, we will take one 1 unit coin. So ultimately the solution of Greedy Method is 31 = 25 + 1 + 1 + 1 + 1 + 1 + 1 (Total 7 nk!umbers of coins needed)

But evidently there is better solution like 31 = 10 + 10 + 10 + 1 (only 4 numbers of coins are needed). 

Hence Greedy Method will never work.

Now let us check whether any better algorithm exists or not! What about the following?

To make K units:

If there is a K unit coin, then that one coin is the minimum

Otherwise, for each value i < K,

Find the minimum number of coins needed to make i units

Find the minimum number of coins needed to make K - i units

Choose the value of i that minimizes this sum

 Yes. This will work. This is actually following Divide & Conquer Principle but there are two problems with this. This solution is very recursive and it requires exponential amount of work to be done.

 Now, if we fix the given set of coins as 1, 5, 10, 21, 25 and if the desired amount is 63, then the previous solution will require solving 62 recursive sub problems. 

What If we think to choose the best solution among?

•   One 1 unit coin plus the best solution for 62 units
•   One 5 units coin plus the best solution for 58 units
•   One 10 units coin plus the best solution for 53 units
•   One 21 units coin plus the best solution for 42 units
•   One 25 units coin plus the best solution for 38 units

In this case, we need to solve only 5 recursive sub problems. So obviously, this second solution is better than the first solution. But still, this second solution is also very expensive. 

Now let us check how DP can solve it!

To make it shorter in length, let us think that desired value is 13 units and the set of coin given is 1 unit, 3 units, and 4 units.

DP solves first for one unit, then two units, then three units, etc., up to the desired amount and saves each answer in a table (Memoization). Hence it goes like

For each new amount N, compute all the possible pairs of previous answers which sum to N

For example, to find the solution for 13 units,

First, solve for all of 1 unit, 2 units, 3 units, ..., 12 units

Next, choose the best solution among:

• Solution for 1unit   +   solution for 12 units
•  Solution for 2 units   +   solution for 11 units
•  Solution for 3 units   +   solution for 10 units
•  Solution for 4 units   +   solution for 9 units
•  Solution for 5 units   +   solution for 8 units
•  Solution for 6 units   +   solution for 7 units

This will run like following:

There’s only one way to make 1unit (one coin)

To make 2 units, try 1 unit +1 unit (one coin + one coin = 2 coins)

To make 3 units, just use the 3 units coin (one coin)

To make 4 units, just use the 4 units coin (one coin)

To make 5 units, try

• 1 unit + 4 units (1 coin + 1 coin = 2 coins)
•  2 units + 3 units (2 coins + 1 coin = 3 coins)
•  The first solution is better, so best solution is 2 coins

To make 6 units, try

•  1 unit + 5 units (1 coin + 2 coins = 3 coins)
•  2 units + 4 units (2 coins + 1 coin = 3 coins)
•  3 units + 3 units (1 coin + 1 coin = 2 coins) – best solution

Etc.

Ok. I got it but how could you say that computationally this is the best?

The first algorithm is recursive, with a branching factor of up to 62. Possibly the average branching factor is somewhere around half of that (31). So the algorithm takes exponential time, with a large base.

The second algorithm is much better—it has a branching factor of 5. Still this is exponential time, with base 5.

The dynamic programming algorithm is O(N*K), where N is the desired amount and K is the number of different kinds of coins. 

So I don’t hesitate to say that computationally, DP algorithm works best among these threes.

What is this Matrix Chain Multiplication Problem?

Suppose we have a sequence or chain A₁, A₂, …, A_n of n matrices to be multiplied. That is, we want to compute the product A₁A₂…A_n. Now there are many possible ways (parenthesizations) to compute the product.

Let us consider the chain A₁, A₂, A₃, A₄ of 4 matrices. Now to compute the product A₁A₂A₃A_4,there are 5 possible ways as described below:

 (A₁(A₂(A₃A₄))), (A₁((A₂A₃)A₄)), ((A₁A₂)(A₃A₄)), ((A₁(A₂A₃))A₄), (((A₁A₂)A₃)A₄)

 Each of these options may lead to the different number of scalar multiplications, and we have to select the best one (option resulting fewer number of Scalar Multiplications)

 Hence the problem statement looks something like:  “Parenthesize the product A₁A₂…A_n such that the total number of scalar multiplications is minimized”

 Please remember that the objective of Matrix Chain Multiplication is not to do the multiplication physically, rather the objective is to fix the way of that multiplication ordering so that the number of scalar multiplication gets minimized.

 Give me one real example:

 Ok. But before I show you one real example, let us revisit the algorithm which multiplies two matrices. It goes like following:

 Input: Matrices A_p×q and B_q×r (with dimensions p×q and q×r)

Result: Matrix C_p×r resulting from the product A·B

MATRIX-MULTIPLY(A_p×q , B_q×r)

1. for i ← 1 to p
2. for j ← 1 to r
3. C[i, j] ← 0
4. for k ← 1 to q
5. C[i, j] ← C[i, j] + A[i, k] · B[k, j]
6. return C

 In the above algorithm, scalar multiplication in line 5 dominates time to compute C Number of scalar multiplications read less

I am sure; you guys are quite familiar with C programming, especially, while it comes to write the first line of your main function. In my class, I have seen many of my students are writing main function with many different forms.

 Some portion of students write like main(), some write main(void), again some of the students write void main(void) and int main(void). Now the question is which one is right?

All are right. Generally you write your C programs with Turbo C editor, or with any other, and generally they do not complain if you write any of them. But still, there is a factor of theoretical perfection. Trivial programming exercises may not be affected with whatever way you follow to declare main function, but in critical cases, your decision may make differences. This is why you should know which one is theoretically perfect.

 As we always know that main is a function which gets called at the beginning of execution of any program. So like other functions, main must have a return type and it must expect arguments. If you are not calling your program (or your main likewise) from the command prompt, your mainfunction should not bother for any arguments, so actually you should call your main with void argument, like main(void).

Now you may raise a point that main() itself suggest that no arguments are passed, so what is wrong with it? See one thing, in your current compiler, the default argument is void, but the same may not be true with other compilers or platforms. So you may end up with portability issues! Keep in mind, A Good Programmer Never Rely On Defaults. So please don’t rely on default things any more, clearly write that your main function is not expecting any arguments by writing main(void).

You already have an idea that a function can never work unless and until it is being called by any other program component. This is true for main also. The function main must be called by someone! Who is that? Who calls main function? It is the operating system who calls main function. Now the thing is, your operating system may decide to do any other job according to the success or failure of running your main function. It may so happen that if your program runs successfully, operating system will call a program P1, and if your program does not work, your operating system will call another program P2. So what if your operating system has no idea that your program did run actually or not? There lies the importance of return type of main. Your main function should return something to your operating system back to indicate whether it has ran successfully or not. The rule is if operating system gets an integer 0 back, it takes as main has ran successfully and any non zero value indicates the opposite. So your main program should return an integer. Hence you should write int main(void). Just to add with this, don’t forget to return 0 at the end of your main program so that, if all of your codes run successfully, your main function is capable of returning 0 to the operating system back, indicating that it was a success.

In this point you may argue, that your programs runs quite well even if you do not provide return type to main and you just write main(void). How come it is possible?

Once again, at your age, you are writing just some of trivial academic codes. The situations here are not such critical that your operating system may decide any other thing depending on the success or failure of your main(). But, in near future, you are to write such critical programs, so get prepared from now.

Cool, so to conclude, int main(void) is perfect to write and I encourage you to write like that along with a return 0 at the last line.  

The difference is indeed very thin and it depends on the context. In general Function is a piece of code with a name, inputs (arguments) and an output (return types). That is function should always return. Some programming languages are there which uniquely maps inputs to the corresponding outputs. But surely C is not such.  There is also a convention (but not a very strict one) that a function should not change any global variable. In C language, a function is always a realistic part of the code.

Subroutine is just a piece of any sorts of code with a definite entry and exit point. It should not return anything and a subroutine can always change global variables. These are generally used for conceptual purposes like in psudocodes.